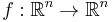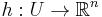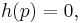Hartman–Grobman theorem

In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point.

Basically the theorem states that the behaviour of a dynamical system near a hyperbolic equilibrium point is qualitatively the same as the behaviour of its linearization near this equilibrium point provided that no eigenvalue of the linearization has its real part equal to 0. Therefore when dealing with such fixed points one can use the simpler linearization of the system to analyze its behaviour.

Main theorem

Let

f: \mathbb{R}^n \to \mathbb{R}^n

be a smooth map with a hyperbolic equilibrium point p, that is : f(p)=0 and no eigenvalue of the linearization A of f at point p has its real part equal to 0. Then there exists a neighborhood U of p and a homeomorphism

h�: U \to \mathbb{R}^n

such that

h(p)=0,\,

and such that in a neighbourhood U of p, the flow of f is topologically conjugate by h to the flow of its linearization A.[1][2][3]

In general, even for infinitely differentiable maps f, the homeomorphism h need not to be smooth, nor even locally Lipschitz. However, it turns out to be Hölder continuous, with an exponent depending on the constant of hyperbolicity of A.

References

  1. ^ Grobman, D. M. (1959). "О гомеоморфизме систем дифференциальных уравнений [Homeomorphisms of systems of differential equations]". Doklady Akademii Nauk SSSR 128: 880–881. 
  2. ^ Hartman, Philip (August 1960). "A lemma in the theory of structural stability of differential equations". Proc. A.M.S. 11 (4): 610–620. doi:10.2307/2034720. JSTOR 2034720. 
  3. ^ Hartman, Philip (1960). "On local homeomorphisms of Euclidean spaces". Bol. Soc. Math. Mexicana 5: 220–241. 

External links